おはようございます、昨日の話です。
この前のJAPLJ contestが3ヶ月ぶりのコンテストでコーディング速度が非常に遅くなっていたので、またリハビリしないとなあと思いながら、SRMなんかも時間が合わなくて中々出れなかった中21:00という久しぶりに参加しやすい時間帯だったので参加したら4時間という長時間で非常に疲れました。因みに今回でyellow(Captain) になりました(・∀・)!
Aは極単純,Bは面倒なだけ,Cはリーディングハード,Dもややリーディングハード,Eは普通,F,Gは読んでません。アルゴリズムの難易度についてはとやかく言える身分じゃないので言及しません。
Eの解法について何人もに訊かれたので、書き留めておきます。
Problem E “Let’s Go Rolling!”
http://codeforces.com/contest/38/problem/E
DPです。右方向にビー玉を追加していきます。今n-1個のビー玉があって、n番目のビー玉を一番右に追加したとします。その時増加するコストは、次のようになります。
ピン留めする→そのビー玉のピン留めコスト分
ピン留めしない→(一番右の)最後にピン留めした位置までの距離
つまり、n-1個までの情報の内、解を求める為に必要な情報は、n-1個の中で最後にピン留めした位置とそのコストです。最後にピン留めした位置が同じならそれ以降の最適解は同じなので、ピン留めした位置毎に最適(最小)な値を残せばいいことになります。
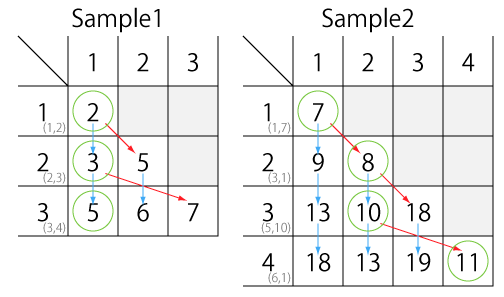
DPテーブル 最後にC++のコードです。図の二次元の表で、新しい行を計算するときには直前の一行の値しか参照していないので、一次元配列を更新していくように実装しています。計算量は変わりません。
#include <iostream>
#include <vector>
#include <algorithm>
#define REP(i,n) for(int i = 0; i < (n); ++i)
#define FOR(i,a,b) for(int i = (a); i < (b); ++i)
#define ALL(cont) (cont).begin(), (cont).end()
using namespace std;
typedef long long ll;
typedef vector<int> vi;
typedef vector<ll> vl;
typedef pair<int, int> pii;
typedef vector<pii> vii;
int main() {
int n;
cin >> n;
vii x(n);
REP(i,n) cin >> x[i].first >> x[i].second;
sort(ALL(x));
vl c(1, x[0].second);
FOR(i,1,n) {
c.push_back(x[i].second + *min_element(ALL(c)));
REP(j,i) c[j] += x[i].first - x[j].first;
}
cout << *min_element(ALL(c)) << endl;
return 0;
}